Graph theory and connectivity of the web
It is useful to visually map the web to better understand the structure. There are many different ways to imagine what the web might look like (including this rather funny map) but there is some academic agreement about:
- bowtie structure
- strongly connected core (SCC)
- diameter
summary[edit]
The web graph is a complex network that exhibits a number of interesting features and characteristics. Some of the main features of the web graph include:
Bowtie structure: The web graph has a bowtie structure, which means that it consists of three main components: a strongly connected core (SCC), a set of in-components, and a set of out-components. The SCC is the part of the graph that is strongly connected, which means that there are paths between any two nodes in the SCC. The in-components and out-components are the parts of the graph that are connected to the SCC, but are not strongly connected.
Strongly connected core (SCC): The SCC is the most central and important part of the web graph, as it represents the web pages and links that are most heavily connected and influential. The SCC is often used as a measure of the connectivity and centrality of the web graph.
Diameter: The diameter of the web graph is a measure of the length of the longest shortest path between any two nodes in the graph. The diameter of the web graph is a useful measure of the size and complexity of the graph, as it gives us a sense of the distance between the most distant nodes in the graph.
Connectivity: The web graph is a highly interconnected network, with many web pages and links connecting different parts of the web. The connectivity of the web graph is an important factor in its functionality and usefulness, as it allows users to easily access and navigate a wide range of content and resources.
Clustering: The web graph exhibits a high degree of clustering, which means that web pages and links tend to be more densely connected within groups or clusters of related content, rather than being evenly distributed throughout the graph.
Power law distribution: The web graph exhibits a power law distribution, which means that a small number of nodes have a disproportionately large number of connections (also known as "hubs"). This can create a skewed distribution of power and influence within the web graph, with a small number of highly connected nodes having a significant impact on the overall structure and connectivity of the graph.
In summary, the web graph is a complex network that exhibits a bowtie structure, with a strongly connected core (SCC), a high degree of connectivity and clustering, and a power law distribution of connections. These features help to shape the structure and functionality of the web, and can have important implications for how the web is used and experienced by users.
Bowtie structure[edit]
It has been suggested we can imagine the web as a bowtie structure (image below). The image below references older number of vertices (nodes) There are many more.
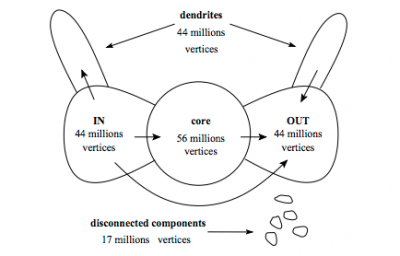
The Bow Tie model comprises four main groups of web pages. There is a strongly connected core. There are then two other large groups, roughly of equal size. One consists of all pages that link to the strongly connected core, but which have no links from the core back out to them. This is the "Origination" or "In" group, as it contains links that lead into the core when originating from it. The counterpart to this is the group of all pages that the strongly connected core links to, but which have no links back into the core. This is the "Termination" or "Out" group, as it contains links that lead out of the core and terminate from it. The fourth and final group is all other disconnected pages, which neither link to the core nor are linked from it.
A more comprehensive representation of the Bow Tie model has been presented with additional, smaller groups of web pages. In this version, both the "In" and "Out" groups have smaller "tendrils" leading to and from them. These consist of pages that link to and from the "In" and "Out" group but are not part of either to begin with, in essence the "Origination" and "Termination" groups of the larger "In" and "Out". This can be carried on ad nauseam, adding tendrils to the tendrils, and so on. Additionally, this more detailed version contains another important group known as the "Tubes". This group consists of pages accessible from "In" and which link to "Out", but which are not part of the large core. Visually, they form alternative routes from "In" to "Out", like tubes bending around the central strongly connected component.[2]
Strongly Connected Core (SCC)[edit]
In the mathematical theory of directed graphs, a graph is said to be strongly connected if every vertex is reachable from every other vertex.[3]. In the context of web science, we use SCC to describe a large cluster of websites that are connected to each other. Imagine the number of shared connections between facebook, google, and reddit. We could imagine this as a center of gravity for the web, and refer to this as a strongly connected core (SCC).
Diameter[edit]
The length of the "longest shortest path" between any two graph vertices of a graph. In other words, a graph's diameter is the largest number of vertices which must be traversed in order to travel from one vertex to another when paths which backtrack, detour, or loop are excluded from consideration. [4]
Diameter: The diameter of a graph is the length of the longest chain you are forced to use to get from one vertex to another in that graph. You can find the diameter of a graph by finding the distance between every pair of vertices and taking the maximum of those distances.[5]
Graphs and determining the connectivity of the web[edit]
We graph the web to model connectivity. We would want to be aware of the number of links to any one cluster of sites, and any nodes which were unlinked. Understanding the nature of relationships between nodes gives us better information to build a more open, democratic web.
Standards[edit]
These standards are used from the IB Computer Science Subject Guide[6]
- Describe the main features of the web graph such as bowtie structure, strongly connected core (SCC), diameter.
- Explain the role of graph theory in determining the connectivity of the web.
References[edit]
- ↑ http://www.flaticon.com/
- ↑ https://en.wikipedia.org/wiki/Internet_topology#Bow_Tie_Model
- ↑ https://en.wikipedia.org/wiki/Strongly_connected_component
- ↑ Weisstein, Eric W. "Graph Diameter." From MathWorld--A Wolfram Web Resource. http://mathworld.wolfram.com/GraphDiameter.html
- ↑ https://stackoverflow.com/questions/3174569/what-is-meant-by-diameter-of-a-network
- ↑ IB Diploma Programme Computer science guide (first examinations 2014). Cardiff, Wales, United Kingdom: International Baccalaureate Organization. January 2012.