Tree: Difference between revisions
Mr. MacKenty (talk | contribs) (Created page with "right|frame|Programming basics<ref>http://www.flaticon.com/</ref> In computer science, a tree is a widely used abstract data type (ADT)—or data structur...") |
Mr. MacKenty (talk | contribs) |
||
| (9 intermediate revisions by the same user not shown) | |||
| Line 6: | Line 6: | ||
== Image of a | == Image of a tree == | ||
[[File: | [[File:Binary tree.svg.png]] | ||
== | == tree vocabulary == | ||
* | * root node | ||
* | * parent node | ||
* | * child node | ||
* | * leaf node | ||
== Practical applications of a tree == | == Practical applications of a tree == | ||
* | * Trees can be used to store data that has an inherent hierarchical structure. For example, an operating system may use a tree for directories, files and folders in its file management system. | ||
* | * They are dynamic, which means that it is easy to add and delete nodes. | ||
* They are easy to search and sort using standard traversal algorithms. | |||
* They can be used to process the syntax of statements in natural and programming languages so are commonly used when compiling programming code. | |||
== Tree - video example == | == Tree - video example == | ||
[https://www.youtube.com/watch?v=qH6yxkw0u78 This video provides a basic introduction to trees. It also summarizes, very nicely, other data structures.] | [https://www.youtube.com/watch?v=qH6yxkw0u78 This video provides a basic introduction to trees. It also summarizes, very nicely, other data structures.] Please keep in mind the example at the beginning is not a [[binary tree]], but binary trees are discussed later. Ignore the discussion about cousins and uncles. It's ridiculous. But the rest of the video is really good. | ||
== code sample == | |||
<syntaxhighlight lang="python"> | |||
class Node: | |||
def __init__(self, data): | |||
self.data = data | |||
self.children = [] | |||
def add_child(self, child): | |||
self.children.append(child) | |||
def __repr__(self): | |||
return f"Node({self.data})" | |||
class Tree: | |||
def __init__(self, root_data): | |||
self.root = Node(root_data) | |||
def add_node(self, parent_data, child_data): | |||
parent_node = self.find_node(parent_data) | |||
if parent_node: | |||
parent_node.add_child(Node(child_data)) | |||
else: | |||
print(f"Parent node with data '{parent_data}' not found.") | |||
def find_node(self, target_data, current_node=None): | |||
if current_node is None: | |||
current_node = self.root | |||
if current_node.data == target_data: | |||
return current_node | |||
for child in current_node.children: | |||
result = self.find_node(target_data, child) | |||
if result: | |||
return result | |||
return None | |||
def display(self, current_node=None, level=0): | |||
if current_node is None: | |||
current_node = self.root | |||
print(' ' * 4 * level + '|-- ' + str(current_node.data)) | |||
for child in current_node.children: | |||
self.display(child, level + 1) | |||
def __repr__(self): | |||
return f"Tree({self.root})" | |||
# Create a tree with root node data 'A' | |||
tree = Tree('A') | |||
# Add nodes to the tree | |||
tree.add_node('A', 'B') | |||
tree.add_node('A', 'C') | |||
tree.add_node('B', 'D') | |||
tree.add_node('B', 'E') | |||
tree.add_node('C', 'F') | |||
tree.add_node('C', 'G') | |||
# Find a node in the tree | |||
found_node = tree.find_node('F') | |||
print(found_node) # Output: Node(F) | |||
# Try to add a node with a nonexistent parent | |||
tree.add_node('X', 'Y') # Output: Parent node with data 'X' not found. | |||
# Display the tree using simple ASCII art | |||
tree.display() | |||
</syntaxhighlight> | |||
== Standards == | == Standards == | ||
| Line 36: | Line 113: | ||
* [[Abstract data structures]] | * [[Abstract data structures]] | ||
* [[binary tree]] | |||
== External Links == | |||
[http://cslibrary.stanford.edu/110/BinaryTrees.html high level discussion of binary trees] | |||
== References == | == References == | ||
Latest revision as of 06:28, 26 April 2023
In computer science, a tree is a widely used abstract data type (ADT)—or data structure implementing this ADT—that simulates a hierarchical tree structure, with a root value and subtrees of children with a parent node, represented as a set of linked nodes.
A tree data structure can be defined recursively (locally) as a collection of nodes (starting at a root node), where each node is a data structure consisting of a value, together with a list of references to nodes (the "children"), with the constraints that no reference is duplicated, and none points to the root.[2]
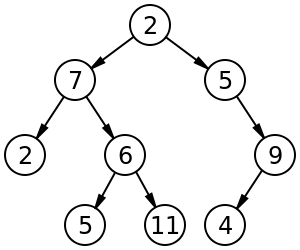
Image of a tree[edit]
tree vocabulary[edit]
- root node
- parent node
- child node
- leaf node
Practical applications of a tree[edit]
- Trees can be used to store data that has an inherent hierarchical structure. For example, an operating system may use a tree for directories, files and folders in its file management system.
- They are dynamic, which means that it is easy to add and delete nodes.
- They are easy to search and sort using standard traversal algorithms.
- They can be used to process the syntax of statements in natural and programming languages so are commonly used when compiling programming code.
Tree - video example[edit]
This video provides a basic introduction to trees. It also summarizes, very nicely, other data structures. Please keep in mind the example at the beginning is not a binary tree, but binary trees are discussed later. Ignore the discussion about cousins and uncles. It's ridiculous. But the rest of the video is really good.
code sample[edit]
class Node:
def __init__(self, data):
self.data = data
self.children = []
def add_child(self, child):
self.children.append(child)
def __repr__(self):
return f"Node({self.data})"
class Tree:
def __init__(self, root_data):
self.root = Node(root_data)
def add_node(self, parent_data, child_data):
parent_node = self.find_node(parent_data)
if parent_node:
parent_node.add_child(Node(child_data))
else:
print(f"Parent node with data '{parent_data}' not found.")
def find_node(self, target_data, current_node=None):
if current_node is None:
current_node = self.root
if current_node.data == target_data:
return current_node
for child in current_node.children:
result = self.find_node(target_data, child)
if result:
return result
return None
def display(self, current_node=None, level=0):
if current_node is None:
current_node = self.root
print(' ' * 4 * level + '|-- ' + str(current_node.data))
for child in current_node.children:
self.display(child, level + 1)
def __repr__(self):
return f"Tree({self.root})"
# Create a tree with root node data 'A'
tree = Tree('A')
# Add nodes to the tree
tree.add_node('A', 'B')
tree.add_node('A', 'C')
tree.add_node('B', 'D')
tree.add_node('B', 'E')
tree.add_node('C', 'F')
tree.add_node('C', 'G')
# Find a node in the tree
found_node = tree.find_node('F')
print(found_node) # Output: Node(F)
# Try to add a node with a nonexistent parent
tree.add_node('X', 'Y') # Output: Parent node with data 'X' not found.
# Display the tree using simple ASCII art
tree.display()
Standards[edit]
- Describe how trees operate logically (both binary and non-binary).
- Define the terms: parent, left-child, right-child, subtree, root and leaf.
- State the result of inorder, postorder and preorder tree traversal.
- Sketch binary trees.
See Also[edit]
External Links[edit]
high level discussion of binary trees