Tree: Difference between revisions
Mr. MacKenty (talk | contribs) (Created page with "right|frame|Programming basics<ref>http://www.flaticon.com/</ref> In computer science, a tree is a widely used abstract data type (ADT)—or data structur...") |
Mr. MacKenty (talk | contribs) |
||
| Line 6: | Line 6: | ||
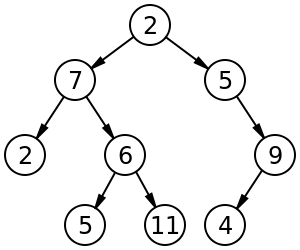
== Image of a | == Image of a tree == | ||
[[File: | [[File:Binary tree.svg.png]] | ||
== Access methods of a tree == | == Access methods of a tree == | ||
Revision as of 14:28, 5 December 2016
Programming basics[1]
In computer science, a tree is a widely used abstract data type (ADT)—or data structure implementing this ADT—that simulates a hierarchical tree structure, with a root value and subtrees of children with a parent node, represented as a set of linked nodes.
A tree data structure can be defined recursively (locally) as a collection of nodes (starting at a root node), where each node is a data structure consisting of a value, together with a list of references to nodes (the "children"), with the constraints that no reference is duplicated, and none points to the root.[2]
Image of a tree[edit]
Access methods of a tree[edit]
- enqueue
- dequeue
- isEmpty
- peek
Practical applications of a tree[edit]
- Printer queues
- Computer modelling of physical queues (like in a supermarket)
Tree - video example[edit]
Standards[edit]
- Describe how trees operate logically (both binary and non-binary).
- Define the terms: parent, left-child, right-child, subtree, root and leaf.
- State the result of inorder, postorder and preorder tree traversal.
- Sketch binary trees.