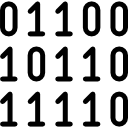Binary: Difference between revisions
Mr. MacKenty (talk | contribs) |
|||
| (40 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
[[File:binary.png|frame|right|This is a basic concept in computer science]] | [[File:binary.png|frame|right|This is a basic concept in computer science]] | ||
In mathematics and digital electronics, a binary number is a number expressed in the binary numeral system or base-2 numeral system which represents numeric values using two different symbols: typically 0 (zero) and 1 (one). The base-2 system is a positional notation with a radix of 2. Because of its straightforward implementation in digital electronic circuitry using logic gates, the binary system is used internally by almost all modern computers and computer-based devices. Each digit is referred to as a bit.<ref>https://en.wikipedia.org/wiki/Binary_number</ref> | |||
== Binary == | == Binary == | ||
This is one of the better videos I've seen on binary. | This is one of the better videos I've seen on binary. Content gratefully used with permission : <ref>http://cs50.tv/2015/fall/#license,psets</ref> | ||
| Line 9: | Line 12: | ||
</html> | </html> | ||
== | == Basic Definitions == | ||
* '''bit''': The bit represents a logical state with one of two possible values | |||
* '''byte''': A group of 8 adjacent binary digits (8 bits), on which a computer operates as a unit | |||
* '''binary''': The binary numeral system is a base 2 number system. | |||
* '''denary/decimal''': The decimal numeral system (also called base 10 or occasionally denary) has ten as its base.<ref>https://en.wikipedia.org/wiki/Decimal</ref> | |||
* '''hexadecimal''': In mathematics and computing, hexadecimal (also base 16, or hex) is a positional numeral system with a radix, or base, of 16<ref>https://en.wikipedia.org/wiki/Hexadecimal</ref>. [https://www.youtube.com/watch?v=nrFHGtGdOzA Click here for an excellent video about hexidecimal] | |||
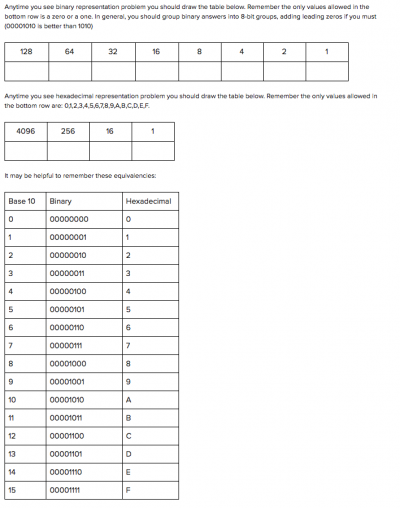
== Binary translation table == | |||
I find it helpful to draw this table when I must convert binary to [[base 10]]. It also helps when looking at the video above. | |||
{| style="width: 95%;" class="wikitable" | {| style="width: 95%;" class="wikitable" | ||
|-style="text-align:center;" | |-style="text-align:center;" | ||
| Line 18: | Line 29: | ||
|} | |} | ||
== | == A helpful cheat sheet == | ||
<br /> | |||
[[File:NumberSystems.png|400px]] | |||
<br /> | |||
== How to add two binary numbers == | |||
Adding binary is straight forward. Line up the numbers as you would if you were adding base-10 numbers. | |||
Remember this: | |||
<code> | |||
0 + 0 = 0 | |||
0 + 1 = 1 | |||
1 + 0 = 1 | |||
1 + 1 = 10, so write a 0 and carry the 1 to the next column. | |||
</code> | |||
== What you must know == | |||
You must be able to correctly answer the following questions: | |||
* Define the term: '''bit''' | |||
* Define the term: '''byte''' | |||
* Define the term: '''binary''' | |||
* Define the term: '''denary/decimal''' (they refer to the same thing) | |||
* Define the term: '''hexadecimal''' | |||
== Why is this so important? == | == Why is this so important? == | ||
If we can represent numbers as '''1 and 0''', why not represent numbers as '''on and off'''? If we can represent letters as numbers (A = 65, B = 66) couldn't we also say A = 01000001 and B = 01000010? | If we can represent numbers as '''1 and 0''', why not represent numbers as '''on and off'''? If we can represent letters as numbers (A = 65, B = 66) couldn't we also say A = 01000001 and B = 01000010? We can follow this line of thinking and make north / south, up / down, and low / high. Simple constructions that we can use to represent more complex numbers and even letters. | ||
Binary representation is the essence of how computers work. | |||
== Resources == | |||
[[Media:9781284069501 PPTx Chapter02.ppt | Click here for a slide deck that covers this topic nicely]] | |||
== References == | |||
<references /> | |||
[[Category: | [[Category:computer organization]] | ||
[[Category:Very important ideas in computer science]] | [[Category:Very important ideas in computer science]] | ||
Latest revision as of 09:07, 22 October 2020
In mathematics and digital electronics, a binary number is a number expressed in the binary numeral system or base-2 numeral system which represents numeric values using two different symbols: typically 0 (zero) and 1 (one). The base-2 system is a positional notation with a radix of 2. Because of its straightforward implementation in digital electronic circuitry using logic gates, the binary system is used internally by almost all modern computers and computer-based devices. Each digit is referred to as a bit.[1]
Binary[edit]
This is one of the better videos I've seen on binary. Content gratefully used with permission : [2]
Basic Definitions[edit]
- bit: The bit represents a logical state with one of two possible values
- byte: A group of 8 adjacent binary digits (8 bits), on which a computer operates as a unit
- binary: The binary numeral system is a base 2 number system.
- denary/decimal: The decimal numeral system (also called base 10 or occasionally denary) has ten as its base.[3]
- hexadecimal: In mathematics and computing, hexadecimal (also base 16, or hex) is a positional numeral system with a radix, or base, of 16[4]. Click here for an excellent video about hexidecimal
Binary translation table[edit]
I find it helpful to draw this table when I must convert binary to base 10. It also helps when looking at the video above.
| 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
|---|---|---|---|---|---|---|---|
A helpful cheat sheet[edit]
How to add two binary numbers[edit]
Adding binary is straight forward. Line up the numbers as you would if you were adding base-10 numbers.
Remember this:
0 + 0 = 0
0 + 1 = 1
1 + 0 = 1
1 + 1 = 10, so write a 0 and carry the 1 to the next column.
What you must know[edit]
You must be able to correctly answer the following questions:
- Define the term: bit
- Define the term: byte
- Define the term: binary
- Define the term: denary/decimal (they refer to the same thing)
- Define the term: hexadecimal
Why is this so important?[edit]
If we can represent numbers as 1 and 0, why not represent numbers as on and off? If we can represent letters as numbers (A = 65, B = 66) couldn't we also say A = 01000001 and B = 01000010? We can follow this line of thinking and make north / south, up / down, and low / high. Simple constructions that we can use to represent more complex numbers and even letters.
Binary representation is the essence of how computers work.
Resources[edit]
Click here for a slide deck that covers this topic nicely