Binary tree: Difference between revisions
Mr. MacKenty (talk | contribs) No edit summary |
Mr. MacKenty (talk | contribs) No edit summary |
||
| (14 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
[[file:arrows.png|right|frame|Programming basics<ref>http://www.flaticon.com/</ref>]] | [[file:arrows.png|right|frame|Programming basics<ref>http://www.flaticon.com/</ref>]] | ||
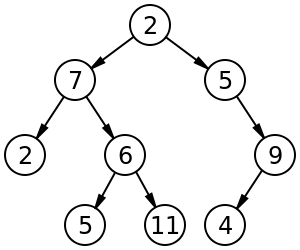
In computer science, a binary tree is a [[tree]] data structure in which each node has at most two children, which are referred to as the left child and the right child.<ref>https://en.wikipedia.org/wiki/Binary_tree</ref> | In computer science, a binary tree is a [[tree]] data structure in which each node has at most two children, which are referred to as the left child and the right child.<ref>https://en.wikipedia.org/wiki/Binary_tree</ref> Please '''do not''' get confused between a binary tree and a binary search tree. | ||
The difference between a binary tree and a binary search tree is '''binary trees are not ordered''' whilst a binary search tree '''is ordered'''. | |||
| Line 10: | Line 12: | ||
== tree vocabulary == | == tree vocabulary == | ||
In addition to NORMAL tree vocabulary: | |||
* root node | * root node | ||
* parent node | * parent node | ||
* child node | * child node | ||
* leaf node | * leaf node | ||
Binary Trees have special vocabulary: | |||
* left-child | |||
* right-child | |||
* subtree | |||
== Practical applications of a tree == | == Practical applications of a tree == | ||
| Line 22: | Line 33: | ||
* They can be used to process the syntax of statements in natural and programming languages so are commonly used when compiling programming code. | * They can be used to process the syntax of statements in natural and programming languages so are commonly used when compiling programming code. | ||
[https://www.youtube.com/watch?v= | == Code sample - binary tree == | ||
<syntaxhighlight lang="python"> | |||
class Node: | |||
def __init__(self, data): | |||
self.data = data | |||
self.left = None | |||
self.right = None | |||
def __repr__(self): | |||
return f"Node({self.data})" | |||
class BinaryTree: | |||
def __init__(self, root_data): | |||
self.root = Node(root_data) | |||
def add_node(self, parent_data, child_data, position): | |||
parent_node = self.find_node(parent_data) | |||
if parent_node: | |||
if position.lower() == 'left': | |||
if parent_node.left is None: | |||
parent_node.left = Node(child_data) | |||
else: | |||
print(f"Parent node '{parent_data}' already has a left child.") | |||
elif position.lower() == 'right': | |||
if parent_node.right is None: | |||
parent_node.right = Node(child_data) | |||
else: | |||
print(f"Parent node '{parent_data}' already has a right child.") | |||
else: | |||
print(f"Invalid position '{position}'. Use 'left' or 'right'.") | |||
else: | |||
print(f"Parent node with data '{parent_data}' not found.") | |||
def find_node(self, target_data, current_node=None): | |||
if current_node is None: | |||
current_node = self.root | |||
if current_node.data == target_data: | |||
return current_node | |||
left_result = self.find_node(target_data, current_node.left) if current_node.left else None | |||
if left_result: | |||
return left_result | |||
right_result = self.find_node(target_data, current_node.right) if current_node.right else None | |||
if right_result: | |||
return right_result | |||
return None | |||
def display(self, current_node=None, level=0): | |||
if current_node is None: | |||
current_node = self.root | |||
if current_node.right: | |||
self.display(current_node.right, level + 1) | |||
print(' ' * 4 * level + '|-- ' + str(current_node.data)) | |||
if current_node.left: | |||
self.display(current_node.left, level + 1) | |||
def __repr__(self): | |||
return f"BinaryTree({self.root})" | |||
# Create a binary tree with root node data 'A' | |||
tree = BinaryTree('A') | |||
# Add nodes to the tree | |||
tree.add_node('A', 'B', 'left') | |||
tree.add_node('A', 'C', 'right') | |||
tree.add_node('B', 'D', 'left') | |||
tree.add_node('B', 'E', 'right') | |||
tree.add_node('C', 'F', 'left') | |||
tree.add_node('C', 'G', 'right') | |||
# Display the tree using simple ASCII art | |||
tree.display() | |||
</syntaxhighlight> | |||
== Binary Tree - video example == | |||
[https://www.youtube.com/watch?v=H5JubkIy_p8 This video provides a basic introduction to binary trees.] | |||
== Traversal == | |||
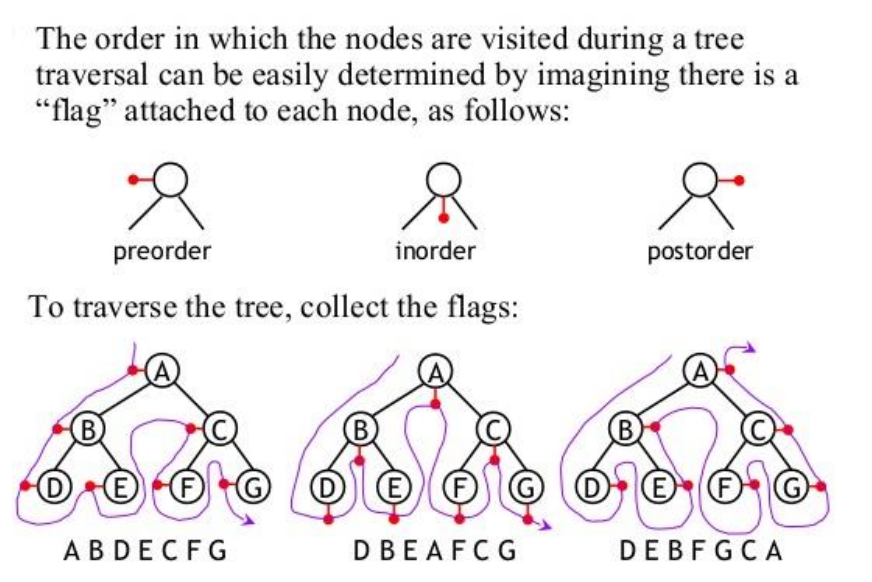
Traversal describes the order in which nodes are visited. I used this image with great gratitude from the guys at Dartford Grammar School<ref>http://ib.compscihub.net/wp-content/uploads/2015/04/5.1.16.pdf</ref> | |||
<br /> | |||
<br /> | |||
[[File:Binary tree traversal.png]] | |||
== Applications of different methods of traversals == | |||
I used these definition from wikipedia <ref>https://en.wikipedia.org/wiki/Tree_traversal#Applications</ref> | |||
* Pre-order traversal while duplicating nodes and edges can make a complete duplicate of a binary tree. It can also be used to make a prefix expression (Polish notation) from expression trees: traverse the expression tree pre-orderly. | |||
* In-order traversal is very commonly used on binary search trees because it returns values from the underlying set in order, according to the comparator that set up the binary search tree (hence the name). | |||
* Post-order traversal while deleting or freeing nodes and values can delete or free an entire binary tree. It can also generate a postfix representation of a binary tree. | |||
== Standards == | == Standards == | ||
| Line 40: | Line 147: | ||
== External Links == | == External Links == | ||
[http://cslibrary.stanford.edu/110/BinaryTrees.html high level discussion of binary trees] | * [http://cslibrary.stanford.edu/110/BinaryTrees.html high level discussion of binary trees] | ||
== References == | == References == | ||
Latest revision as of 06:41, 26 April 2023
Programming basics[1]
In computer science, a binary tree is a tree data structure in which each node has at most two children, which are referred to as the left child and the right child.[2] Please do not get confused between a binary tree and a binary search tree.
The difference between a binary tree and a binary search tree is binary trees are not ordered whilst a binary search tree is ordered.
Image of a tree[edit]
tree vocabulary[edit]
In addition to NORMAL tree vocabulary:
- root node
- parent node
- child node
- leaf node
Binary Trees have special vocabulary:
- left-child
- right-child
- subtree
Practical applications of a tree[edit]
- Trees can be used to store data that has an inherent hierarchical structure. For example, an operating system may use a tree for directories, files and folders in its file management system.
- They are dynamic, which means that it is easy to add and delete nodes.
- They are easy to search and sort using standard traversal algorithms.
- They can be used to process the syntax of statements in natural and programming languages so are commonly used when compiling programming code.
Code sample - binary tree[edit]
class Node:
def __init__(self, data):
self.data = data
self.left = None
self.right = None
def __repr__(self):
return f"Node({self.data})"
class BinaryTree:
def __init__(self, root_data):
self.root = Node(root_data)
def add_node(self, parent_data, child_data, position):
parent_node = self.find_node(parent_data)
if parent_node:
if position.lower() == 'left':
if parent_node.left is None:
parent_node.left = Node(child_data)
else:
print(f"Parent node '{parent_data}' already has a left child.")
elif position.lower() == 'right':
if parent_node.right is None:
parent_node.right = Node(child_data)
else:
print(f"Parent node '{parent_data}' already has a right child.")
else:
print(f"Invalid position '{position}'. Use 'left' or 'right'.")
else:
print(f"Parent node with data '{parent_data}' not found.")
def find_node(self, target_data, current_node=None):
if current_node is None:
current_node = self.root
if current_node.data == target_data:
return current_node
left_result = self.find_node(target_data, current_node.left) if current_node.left else None
if left_result:
return left_result
right_result = self.find_node(target_data, current_node.right) if current_node.right else None
if right_result:
return right_result
return None
def display(self, current_node=None, level=0):
if current_node is None:
current_node = self.root
if current_node.right:
self.display(current_node.right, level + 1)
print(' ' * 4 * level + '|-- ' + str(current_node.data))
if current_node.left:
self.display(current_node.left, level + 1)
def __repr__(self):
return f"BinaryTree({self.root})"
# Create a binary tree with root node data 'A'
tree = BinaryTree('A')
# Add nodes to the tree
tree.add_node('A', 'B', 'left')
tree.add_node('A', 'C', 'right')
tree.add_node('B', 'D', 'left')
tree.add_node('B', 'E', 'right')
tree.add_node('C', 'F', 'left')
tree.add_node('C', 'G', 'right')
# Display the tree using simple ASCII art
tree.display()
Binary Tree - video example[edit]
This video provides a basic introduction to binary trees.
Traversal[edit]
Traversal describes the order in which nodes are visited. I used this image with great gratitude from the guys at Dartford Grammar School[3]
Applications of different methods of traversals[edit]
I used these definition from wikipedia [4]
- Pre-order traversal while duplicating nodes and edges can make a complete duplicate of a binary tree. It can also be used to make a prefix expression (Polish notation) from expression trees: traverse the expression tree pre-orderly.
- In-order traversal is very commonly used on binary search trees because it returns values from the underlying set in order, according to the comparator that set up the binary search tree (hence the name).
- Post-order traversal while deleting or freeing nodes and values can delete or free an entire binary tree. It can also generate a postfix representation of a binary tree.
Standards[edit]
- Describe how trees operate logically (both binary and non-binary).
- Define the terms: parent, left-child, right-child, subtree, root and leaf.
- State the result of inorder, postorder and preorder tree traversal.
- Sketch binary trees.