Tree

Programming basics

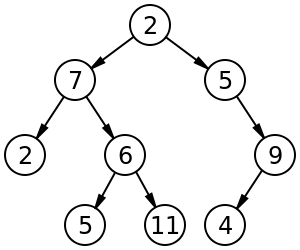
In computer science, a tree is a widely used abstract data type (ADT)—or data structure implementing this ADT—that simulates a hierarchical tree structure, with a root value and subtrees of children with a parent node, represented as a set of linked nodes.

A tree data structure can be defined recursively (locally) as a collection of nodes (starting at a root node), where each node is a data structure consisting of a value, together with a list of references to nodes (the "children"), with the constraints that no reference is duplicated, and none points to the root.

Image of a tree

Access methods of a tree

• enqueue
• dequeue
• isEmpty
• peek

Practical applications of a tree

• Printer queues
• Computer modelling of physical queues (like in a supermarket)

Tree - video example

This video provides a basic introduction to trees. It also summarizes, very nicely, other data structures. Please keep in mind the example is not binary tree, which is different. Ignore the discussion about cousins and uncles. It's ridiculous. But the rest of the video is good.

Standards

• Describe how trees operate logically (both binary and non-binary).
• Define the terms: parent, left-child, right-child, subtree, root and leaf.
• State the result of inorder, postorder and preorder tree traversal.
• Sketch binary trees.

See Also

• Abstract data structures

Give a sequence of brief answers with no explanation.

Give a detailed account or picture of a situation, event, pattern or process.

Give the precise meaning of a word, phrase, concept or physical quantity.

Give a specific name, value or other brief answer without explanation or calculation.

Give a specific name, value or other brief answer without explanation or calculation.

Represent by means of a diagram or graph (labelled as appropriate). The sketch should give a general idea of the required shape or relationship, and should include relevant features.