Recursion: Difference between revisions
Mr. MacKenty (talk | contribs) (Created page with "right|frame|Programming basics<ref>http://www.flaticon.com/</ref> Recursion in computer science is a method where the solution to a problem depends on sol...") |
Mr. MacKenty (talk | contribs) |
||
| Line 6: | Line 6: | ||
== | == Recurion == | ||
<html> | |||
<iframe width="560" height="315" src="https://www.youtube.com/embed/t4MSwiqfLaY" frameborder="0" allowfullscreen></iframe> | |||
</html> | |||
== tree vocabulary == | == tree vocabulary == | ||
Revision as of 08:21, 15 December 2016
Programming basics[1]
Recursion in computer science is a method where the solution to a problem depends on solutions to smaller instances of the same problem (as opposed to iteration). The approach can be applied to many types of problems, and recursion is one of the central ideas of computer science [2]
A simple definition: Recursion is the process of a subroutine calling itself.
Recurion[edit]
tree vocabulary[edit]
In addition to NORMAL tree vocabulary:
- root node
- parent node
- child node
- leaf node
Binary Trees have special vocabulary:
- left-child
- right-child
- subtree
Practical applications of a tree[edit]
- Trees can be used to store data that has an inherent hierarchical structure. For example, an operating system may use a tree for directories, files and folders in its file management system.
- They are dynamic, which means that it is easy to add and delete nodes.
- They are easy to search and sort using standard traversal algorithms.
- They can be used to process the syntax of statements in natural and programming languages so are commonly used when compiling programming code.
Binary Tree - video example[edit]
This video provides a basic introduction to binary trees.
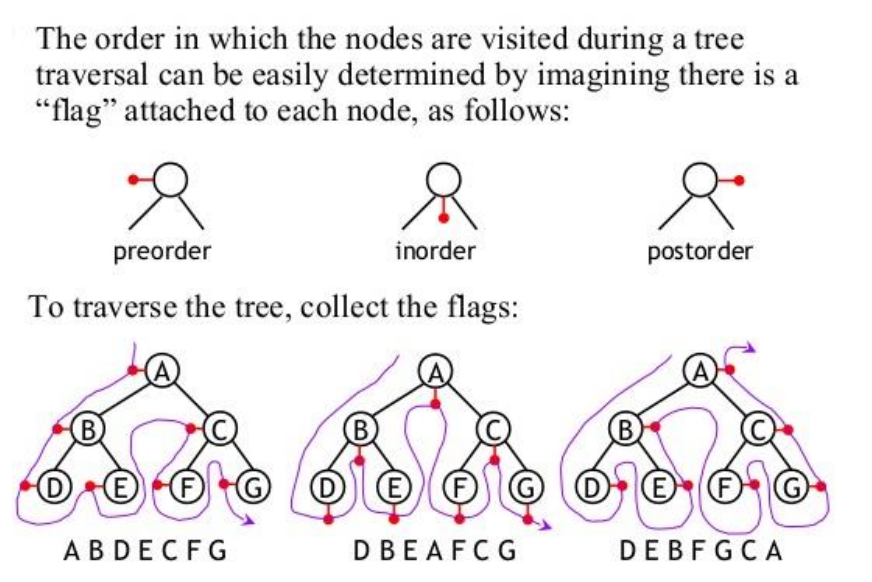
Traversal[edit]
Traversal describes the order in which nodes are visited. I used this image with great gratitude from the guys at Dartford Grammar School[3]
Applications of different methods of traversals[edit]
I used these definition from wikipedia [4]
- Pre-order traversal while duplicating nodes and edges can make a complete duplicate of a binary tree. It can also be used to make a prefix expression (Polish notation) from expression trees: traverse the expression tree pre-orderly.
- In-order traversal is very commonly used on binary search trees because it returns values from the underlying set in order, according to the comparator that set up the binary search tree (hence the name).
- Post-order traversal while deleting or freeing nodes and values can delete or free an entire binary tree. It can also generate a postfix representation of a binary tree.
Standards[edit]
- Identify a situation that requires the use of recursive thinking.
- Identify recursive thinking in a specified problem solution.
- Trace a recursive algorithm to express a solution to a problem.
See Also[edit]
External Links[edit]
high level discussion of binary trees