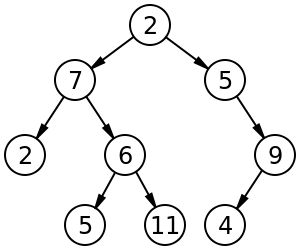
Binary tree
In computer science, a tree is a widely used abstract data type (ADT)—or data structure implementing this ADT—that simulates a hierarchical tree structure, with a root value and subtrees of children with a parent node, represented as a set of linked nodes.
A tree data structure can be defined recursively (locally) as a collection of nodes (starting at a root node), where each node is a data structure consisting of a value, together with a list of references to nodes (the "children"), with the constraints that no reference is duplicated, and none points to the root.[2]
Image of a tree[edit]
tree vocabulary[edit]
- root node
- parent node
- child node
- leaf node
Practical applications of a tree[edit]
- Trees can be used to store data that has an inherent hierarchical structure. For example, an operating system may use a tree for directories, files and folders in its file management system.
- They are dynamic, which means that it is easy to add and delete nodes.
- They are easy to search and sort using standard traversal algorithms.
- They can be used to process the syntax of statements in natural and programming languages so are commonly used when compiling programming code.
Tree - video example[edit]
This video provides a basic introduction to trees. It also summarizes, very nicely, other data structures. Please keep in mind the example at the beginning is not a binary tree, but binary trees are discussed later. Ignore the discussion about cousins and uncles. It's ridiculous. But the rest of the video is really good.
Standards[edit]
- Describe how trees operate logically (both binary and non-binary).
- Define the terms: parent, left-child, right-child, subtree, root and leaf.
- State the result of inorder, postorder and preorder tree traversal.
- Sketch binary trees.
See Also[edit]
External Links[edit]
high level discussion of binary trees