Tree

Programming basics^[1]

In computer science, a tree is a widely used abstract data type (ADT)—or data structure implementing this ADT—that simulates a hierarchical tree structure, with a root value and subtrees of children with a parent node, represented as a set of linked nodes.

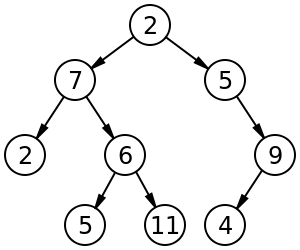
A tree data structure can be defined recursively (locally) as a collection of nodes (starting at a root node), where each node is a data structure consisting of a value, together with a list of references to nodes (the "children"), with the constraints that no reference is duplicated, and none points to the root.^[2]

Image of a tree[edit]

tree vocabulary[edit]

root node
parent node
child node
leaf node

Practical applications of a tree[edit]

Trees can be used to store data that has an inherent hierarchical structure. For example, an operating system may use a tree for directories, files and folders in its file management system.
They are dynamic, which means that it is easy to add and delete nodes.
They are easy to search and sort using standard traversal algorithms.
They can be used to process the syntax of statements in natural and programming languages so are commonly used when compiling programming code.

Tree - video example[edit]

This video provides a basic introduction to trees. It also summarizes, very nicely, other data structures. Please keep in mind the example at the beginning is not a binary tree, but binary trees are discussed later. Ignore the discussion about cousins and uncles. It's ridiculous. But the rest of the video is really good.

code sample[edit]

class Node:
    def __init__(self, data):
        self.data = data
        self.children = []

    def add_child(self, child):
        self.children.append(child)

    def __repr__(self):
        return f"Node({self.data})"

class Tree:
    def __init__(self, root_data):
        self.root = Node(root_data)

    def add_node(self, parent_data, child_data):
        parent_node = self.find_node(parent_data)
        if parent_node:
            parent_node.add_child(Node(child_data))
        else:
            print(f"Parent node with data '{parent_data}' not found.")

    def find_node(self, target_data, current_node=None):
        if current_node is None:
            current_node = self.root

        if current_node.data == target_data:
            return current_node

        for child in current_node.children:
            result = self.find_node(target_data, child)
            if result:
                return result

        return None

    def display(self, current_node=None, level=0):
        if current_node is None:
            current_node = self.root

        print(' ' * 4 * level + '|-- ' + str(current_node.data))
        for child in current_node.children:
            self.display(child, level + 1)



    def __repr__(self):
        return f"Tree({self.root})"

# Create a tree with root node data 'A'
tree = Tree('A')

# Add nodes to the tree
tree.add_node('A', 'B')
tree.add_node('A', 'C')
tree.add_node('B', 'D')
tree.add_node('B', 'E')
tree.add_node('C', 'F')
tree.add_node('C', 'G')

# Find a node in the tree
found_node = tree.find_node('F')
print(found_node)  # Output: Node(F)

# Try to add a node with a nonexistent parent
tree.add_node('X', 'Y')  # Output: Parent node with data 'X' not found.

# Display the tree using simple ASCII art
tree.display()

Standards[edit]

Describe how trees operate logically (both binary and non-binary).
Define the terms: parent, left-child, right-child, subtree, root and leaf.
State the result of inorder, postorder and preorder tree traversal.
Sketch binary trees.

External Links[edit]

high level discussion of binary trees

References[edit]

[1] ttp://www.flaticon.com/

[2] ttps://en.wikipedia.org/wiki/Tree_(data_structure)

[1]

[2]