Abstract data structures

In computer science, an abstract data type (ADT) is a mathematical model for data types where a data type is defined by its behavior (semantics) from the point of view of a user of the data, specifically in terms of possible values, possible operations on data of this type, and the behavior of these operations. This contrasts with data structures, which are concrete representations of data, and are the point of view of an implementer, not a user.
Formally, an ADT may be defined as a "class of objects whose logical behavior is defined by a set of values and a set of operations"; this is analogous to an algebraic structure in mathematics. What is meant by "behavior" varies by author, with the two main types of formal specifications for behavior being axiomatic (algebraic) specification and an abstract model; these correspond to axiomatic semantics and operational semantics of an abstract machine, respectively. Some authors also include the computational complexity ("cost"), both in terms of time (for computing operations) and space (for representing values).[2]
The reason we use abstract structures is because they efficiently use memory based on the design of the data stored in them. With very large amounts of data or very frequently changing data, the data structure can make a huge difference in the efficiency (run time) of your computer program.
In more common language, an abstract data structure is just some arrangement of data that we've built into an orderly arrangement.
A perfectly lovely overview[edit]
Some types of abstract data structures[edit]
- arrays
- two-dimensional arrays
- stack
- queue
- linked list
- tree
- binary tree
- collections
- lists
- dictionaries
- sets
- tuple
We might use recursion to move through an abstract data structure.
Basic operations of data structures[edit]
I found this excellent slide from Simon Allardice.
Comparison of different data structures[edit]
| Data Structure | Strengths | Weaknesses |
| arrays | Inserting and deleting elements, iterating through the collection | Sorting and searching, Inserting and deleting - especially if you are inserting and deleting at the beginning or the end of the array |
| linked list | direct indexing, Easy to create and use | direct access, searching and sorting |
| stack and queue | designed for LIFO / FIFO | direct access, searching and sorting |
| binary tree | speed of insertion and deletion, speed of access, maintaining sorted order | some overhead |
- Fixed structures are faster / smaller
- When you are considering if you should use an abstract data structure, you should ask yourself: what holds the most data and what holds the most frequently changed data?
Comparison of static vs dynamic data structures[edit]
This comparison is used from our computer science textbook.
| Static data structure | Dynamic data structure |
| Inefficient as memory is allocated that may not be needed. | Efficient as the amount of memory varies as needed. |
| Fast access to each element of data as the memory location is fixed when the program is written. | Slower access to each element as the memory location is allocated at run-time. |
| Memory addresses allocated will be contiguous so quicker to access. | Memory addresses allocated may be fragmented so slower to access. |
| Structures are a fixed size, making them more predictable to work with. For example, they can contain a header. | Structures vary in size so there needs to be a mechanism for knowing the size of the current structure. |
| The relationship between different elements of data does not change. | The relationship between different elements of data will change as the program is run. |
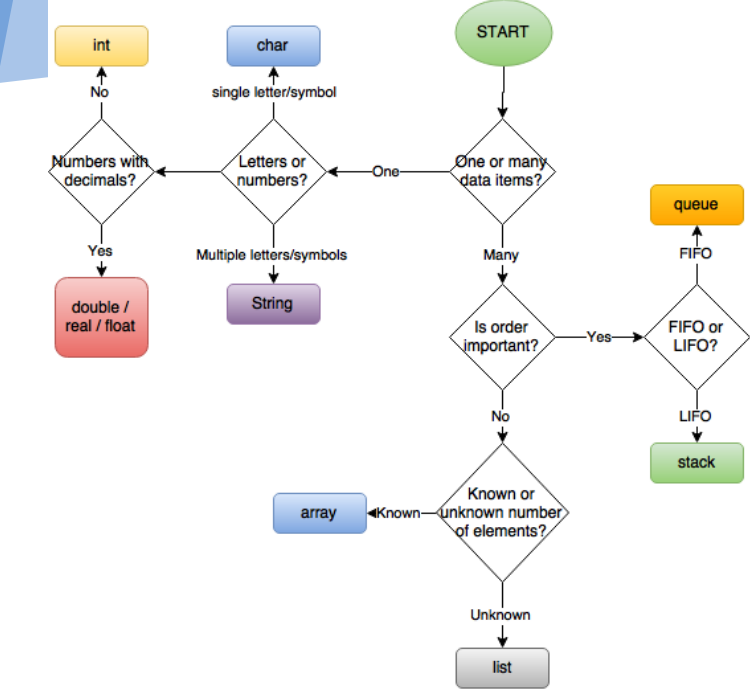
Choosing which data structure to use[edit]
This graphic is used with tremendous gratitude from Dartford Grammar School Computer Science Department.
Other helpful resources[edit]
- Please do look at this page it is excellent introduction to different data structures.
Standards[edit]
- Identify a situation that requires the use of recursive thinking.
- Identify recursive thinking in a specified problem solution.
- Trace a recursive algorithm to express a solution to a problem.
- Describe the characteristics of a two- dimensional array.
- Construct algorithms using two- dimensional arrays.
- Describe the characteristics and applications of a stack.
- Construct algorithms using the access methods of a stack.
- Describe the characteristics and applications of a queue.
- Construct algorithms using the access methods of a queue.
- Explain the use of arrays as static stacks and queues.
- Describe the features and characteristics of a dynamic data structure.
- Describe how linked lists operate logically.
- Sketch linked lists (single, double and circular).
- Describe the characteristics and applications of a collection.
- Construct algorithms using the access methods of a collection.
- Discuss the need for sub-programmes and collections within programmed solutions.
- Construct algorithms using pre-defined sub-programmes, one-dimensional arrays and/or collections.
- Describe how trees operate logically (both binary and non-binary).
- Define the terms: parent, left-child, right-child, subtree, root and leaf.
- State the result of inorder, postorder and preorder tree traversal.
- Sketch binary trees.
- Define the term dynamic data structure.
- Compare the use of static and dynamic data structures.
- Suggest a suitable structure for a given situation.