Recursion: Difference between revisions

From Computer Science Wiki
No edit summary
 
(6 intermediate revisions by the same user not shown)
Line 5: Line 5:
A simple definition: Recursion is the process of a subroutine calling itself.
A simple definition: Recursion is the process of a subroutine calling itself.


== Example ==


== Recurion ==  
<syntaxhighlight lang=python>
def factorial(n):
    if n == 1:
        return 1
    else:
        return n * factorial(n-1)
</syntaxhighlight>


== Identify a situation that requires the use of recursive thinking ==
Recursive thinking is a powerful tool that is useful in a variety of situations. Recursive thinking involves breaking a problem down into smaller and smaller subproblems until the subproblems are simple enough to solve directly. Here is an example of a situation that requires the use of recursive thinking:


<html>
Computing factorials:
<iframe width="560" height="315" src="https://www.youtube.com/embed/t4MSwiqfLaY" frameborder="0" allowfullscreen></iframe>
Factorial is a mathematical operation that is denoted by the symbol "!". For a non-negative integer n, n! is defined as the product of all positive integers less than or equal to n. For example, 5! = 5 × 4 × 3 × 2 × 1 = 120.
</html>


== tree vocabulary ==
To compute the factorial of a number n using recursive thinking, we can use the following algorithm:


In addition to NORMAL tree vocabulary:
<syntaxhighlight lang="javascript">


* root node
function factorial(n) {
* parent node
  if (n === 0 || n === 1) {
* child node
    return 1;
* leaf node
  } else {
    return n * factorial(n - 1);
  }
}


Binary Trees have special vocabulary:
</syntaxhighlight>
In this algorithm, we check if n is either 0 or 1. If it is, we return 1 since the factorial of 0 or 1 is 1. Otherwise, we compute n * factorial(n - 1) which calls the factorial function recursively with a smaller value of n. This process continues until n is reduced to 0 or 1, at which point the recursion stops and the final result is returned.


Note that the recursive algorithm for computing factorials is elegant and concise. However, it may not be the most efficient way to compute factorials for very large values of n. In those cases, an iterative algorithm may be more appropriate. Nonetheless, the recursive algorithm demonstrates the power of recursive thinking and how it can be used to solve problems in a concise and elegant way.


* left-child
* right-child
* subtree


== Practical applications of a tree ==  
== Recursion ==  


* Trees can be used to store data that has an inherent hierarchical structure. For example, an operating system may use a tree for directories, files and folders in its file management system.
* They are dynamic, which means that it is easy to add and delete nodes.
* They are easy to search and sort using standard traversal algorithms.
* They can be used to process the syntax of statements in natural and programming languages so are commonly used when compiling programming code.


== Binary Tree - video example ==  
<html>
<iframe width="560" height="315" src="https://www.youtube.com/embed/t4MSwiqfLaY" frameborder="0" allowfullscreen></iframe>
</html>


[https://www.youtube.com/watch?v=H5JubkIy_p8  This video provides a basic introduction to binary trees.]
== Another look at recursion ==


== Traversal ==
<html>
Traversal describes the order in which nodes are visited.  I used this image with great gratitude from the guys at Dartford Grammar School<ref>http://ib.compscihub.net/wp-content/uploads/2015/04/5.1.16.pdf</ref>
<iframe width="560" height="315" src="https://www.youtube.com/embed/VrrnjYgDBEk" frameborder="0" allowfullscreen></iframe>
 
</html>
<br />
<br />
[[File:Binary tree traversal.png]]
 
== Applications of different methods of traversals ==
I used these definition from wikipedia <ref>https://en.wikipedia.org/wiki/Tree_traversal#Applications</ref>


* Pre-order traversal while duplicating nodes and edges can make a complete duplicate of a binary tree. It can also be used to make a prefix expression (Polish notation) from expression trees: traverse the expression tree pre-orderly.
* In-order traversal is very commonly used on binary search trees because it returns values from the underlying set in order, according to the comparator that set up the binary search tree (hence the name).
* Post-order traversal while deleting or freeing nodes and values can delete or free an entire binary tree. It can also generate a postfix representation of a binary tree.


== Standards ==  
== Standards ==  
Line 63: Line 62:


* [[Abstract data structures]]
* [[Abstract data structures]]
== External Links ==
[http://cslibrary.stanford.edu/110/BinaryTrees.html high level discussion of binary trees]


== References ==
== References ==

Latest revision as of 09:45, 9 May 2023

Programming basics[1]

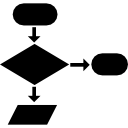
Recursion in computer science is a method where the solution to a problem depends on solutions to smaller instances of the same problem (as opposed to iteration). The approach can be applied to many types of problems, and recursion is one of the central ideas of computer science [2]

A simple definition: Recursion is the process of a subroutine calling itself.

Example[edit]

def factorial(n):
    if n == 1:
        return 1
    else:
        return n * factorial(n-1)

Identify a situation that requires the use of recursive thinking[edit]

Recursive thinking is a powerful tool that is useful in a variety of situations. Recursive thinking involves breaking a problem down into smaller and smaller subproblems until the subproblems are simple enough to solve directly. Here is an example of a situation that requires the use of recursive thinking:

Computing factorials: Factorial is a mathematical operation that is denoted by the symbol "!". For a non-negative integer n, n! is defined as the product of all positive integers less than or equal to n. For example, 5! = 5 × 4 × 3 × 2 × 1 = 120.

To compute the factorial of a number n using recursive thinking, we can use the following algorithm: 

function factorial(n) {
  if (n === 0 || n === 1) {
    return 1;
  } else {
    return n * factorial(n - 1);
  }
}

In this algorithm, we check if n is either 0 or 1. If it is, we return 1 since the factorial of 0 or 1 is 1. Otherwise, we compute n * factorial(n - 1) which calls the factorial function recursively with a smaller value of n. This process continues until n is reduced to 0 or 1, at which point the recursion stops and the final result is returned.

Note that the recursive algorithm for computing factorials is elegant and concise. However, it may not be the most efficient way to compute factorials for very large values of n. In those cases, an iterative algorithm may be more appropriate. Nonetheless, the recursive algorithm demonstrates the power of recursive thinking and how it can be used to solve problems in a concise and elegant way.


Recursion[edit]

Another look at recursion[edit]


Standards[edit]

  • Identify a situation that requires the use of recursive thinking.
  • Identify recursive thinking in a specified problem solution.
  • Trace a recursive algorithm to express a solution to a problem.

See Also[edit]

References[edit]

  1. ↑ http://www.flaticon.com/
  2. ↑ https://en.wikipedia.org/wiki/Recursion_(computer_science)

Provide an answer from a number of possibilities. Recognize and state briefly a distinguishing fact or feature.

A natural number, a negative of a natural number, or zero.

A unit of abstract mathematical system subject to the laws of arithmetic.

Follow and record the action of an algorithm.

Retrieved from "https://computersciencewiki.org/index.php?title=Recursion&oldid=12094"